La forzante radiativa in quattro casi concreti

In IPCC AR5, capitolo 8 SM (Supplementary Material) “Anthropogenic and Natural Radiative Forcing”, a pagina 8SM-7 viene presentata, tra le altre, la formula del forcing radiativo ΔF (indicato anche come RF, in W/m2) per la CO2

ΔF=5.35 x ln(C/Co)		(1)

con C concentrazione attuale di CO2, in ppm, e Co concentrazione di riferimento (qui si usa quella pre-industriale del 1760, pari a 280 ppm).
Seim e Olsen (2020), nella descrizione di un interessante esperimento per verificare sperimentalmente il riscaldamento aggiuntivo dell’atmosfera ad opera dei gas serra, riportano altre formule collegate alla (1)

ΔT=λ ΔF		(2)

dove ΔF è l’aumento della radiazione (in W/m2) diffusa all’indietro dalla CO2 (effetto serra). La costante λ, viene detto, vale circa 0.8.
Ancora in AR5 si stima che un raddoppio della CO2 in aria comporti un forcing infrarosso (IR) di 3.7 W/m2 e un aumento di temperatura di circa 3°C. Infatti:

ΔF= 5.35 x ln(2) = 3.708 W/m2

ΔT= 0.8 x 3.708 = 2.967 °C

Dalla sostituzione della (1) nella (2) si ottiene

ΔT= λ x 5.35 x ln(C/Co)		(3)

ovvero:

ΔT= slope x ln(C/Co)		(3a)

cioè una relazione lineare tra variazione di temperatura ΔT e logaritmo naturale del rapporto tra le concentrazioni della CO2 attuale e quella di riferimento.
Questa relazione è alla base delle affermazioni che stabiliscono la necessità di evitare le emissioni di CO2 in atmosfera per limitare l’aumento di temperatura del pianeta.

Mi propongo qui di verificare la relazione (3a) su estensioni temporali diverse (anche molto grandi), utilizzando anche i dati di prossimità sia per la temperatura (δ18O) che per l’anidride carbonica (carote antartiche). Il confronto viene realizzato su quattro intervalli temporali:

1981-2012, tra l’anomalia di temperatura globale terra+oceano di GHCN (NOAA) di gennaio 2021 (file 2101t.dat) e la CO2 di Mauna Loa (Hawaii), entrambi a passo mensile (file diff12-co2.dat). L’estensione è di 32 anni.
1976-2019, tra la stessa serie di temperatura (2101t.dat) e la CO2 di Mauna Loa (mlo69-19.txt). L’estensione è di 44 anni.
50-0 Ka, tra i dati mostrati in precedenza su http://www.climatemonitor.it/?p=52003, lo18o_td.txt e antarctica2015co2composite.txt della stazione antartica russa, Vostok. L’estensione è pari a 50 mila anni. Le due serie hanno passo diverso, il che rende complicato il confronto, per cui entrambe sono state digitalizzate ad un passo costante di 20 pixel, pari a 1052 anni (~1 kyr), per ottenere i due file effettivamente usati nel confronto, co2-dig.txt e d18o-dig.txt. Queste serie sono indicate come “Vostok”.
424-3 Ma, tra CO2 e δ18O digitalizzate dalla figura di Davis (2017). L’estensione temporale è di 421 milioni di anni. Nel seguito queste serie sono indicate con “Davis”.

Nel caso di “Vostok” il ΔT dell’equazione (3a) viene calcolato come singolo valore di d18O meno la media dell’intera serie, cioè è lo scarto dalla media.
Nel caso di “Davis” il ΔT è il detrended di d18O, ovvero lo scarto dal fit lineare della serie.
In tutti i casi, come valore di riferimento per la concentrazione di CO2 viene usato 280 ppm.
Nel sito di supporto sono disponibili i grafici delle singole equazioni (3a) mentre qui mostro le quattro relazioni raggruppate.

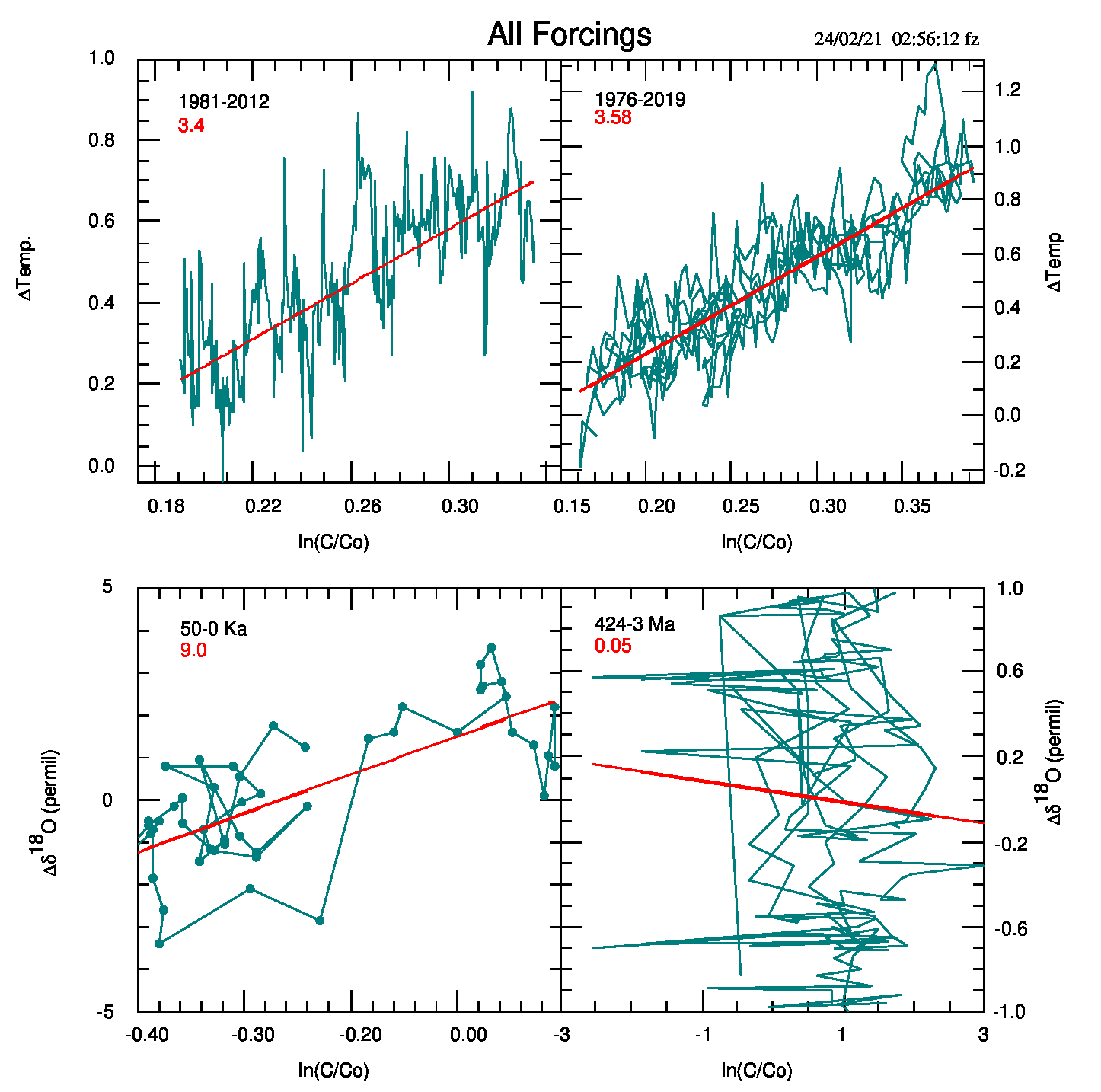
Fig.1: L’equazione (3a) nei quattro casi considerati. Sono riportati i limiti temporali delle serie e, in rosso, la pendenza e il grafico della retta interpolante i dati. Le unità della pendenza sono °C oppure ‰ / ln(ppm)

Dalle equazioni (3) e (3a) segue che la costante λ può essere calcolata a posteriori come λ=slope/5.35 e i valori della pendenza riportati in rosso nella figura 1 permettono di verificare che λ per i quattro casi vale 0.63 e 0.67 (°C m2/W); 1.68 e 0.009 (permille m2/W).
La relazione (3a) si verifica, come andamento medio, per tre delle quattro estensioni temporali ma, a parte il primo caso di 32 anni, la relazione media viene generata attraverso una complicata serie di avanzamenti e arretramenti (ghirigori o disegni casuali) che non fanno pensare ad un rapporto diretto tra aumento della concentrazione di CO2 e temperatura. La natura delle serie, specialmente le più estese, può generare (e ha generato) dubbi sull’effettivo allineamento temporale delle due variabili: voglio sottolineare che è stata posta un’attenzione particolare nel verificare questo allineamento.

A titolo di curiosità (ma non troppo) propongo, in tabella 1, una selezione di corrispondenze tra i massimi e i minimi dei due quadri superiori di figura 1 e gli eventi (El Nino, La Nina):

**Table 1:** El Nino or La Nina events for a selection of ouliers in 1981-2012 and 1976-2019 series (figure 1). Compare to http://ggweather.com/enso/oni.htm
ln(C/Co)	CO2	Evento	Carattere
		1981-2012
0.196	340.6	1982, El Nino	molto forte
0.223	349.9	1987-88, El Nino	forte
0.246	358.1	1995-96, La Nina	debole
0.262	363.9	1997-98, El Nino	molto forte
0.315	383.7	2007, La Nina	moderato
0.325	387.5	2010, El Nino	molto forte
		1976-2019
0.180	335.2	1977-78, El Nino	debole
0.205	343.7	1982-83, El Nino	molto forte
0.270	366.8	1997-98, El Nino	molto forte
0.320	385.6	2007-08, La Nina	moderato
0.370	405.4	2016, El Nino	forte

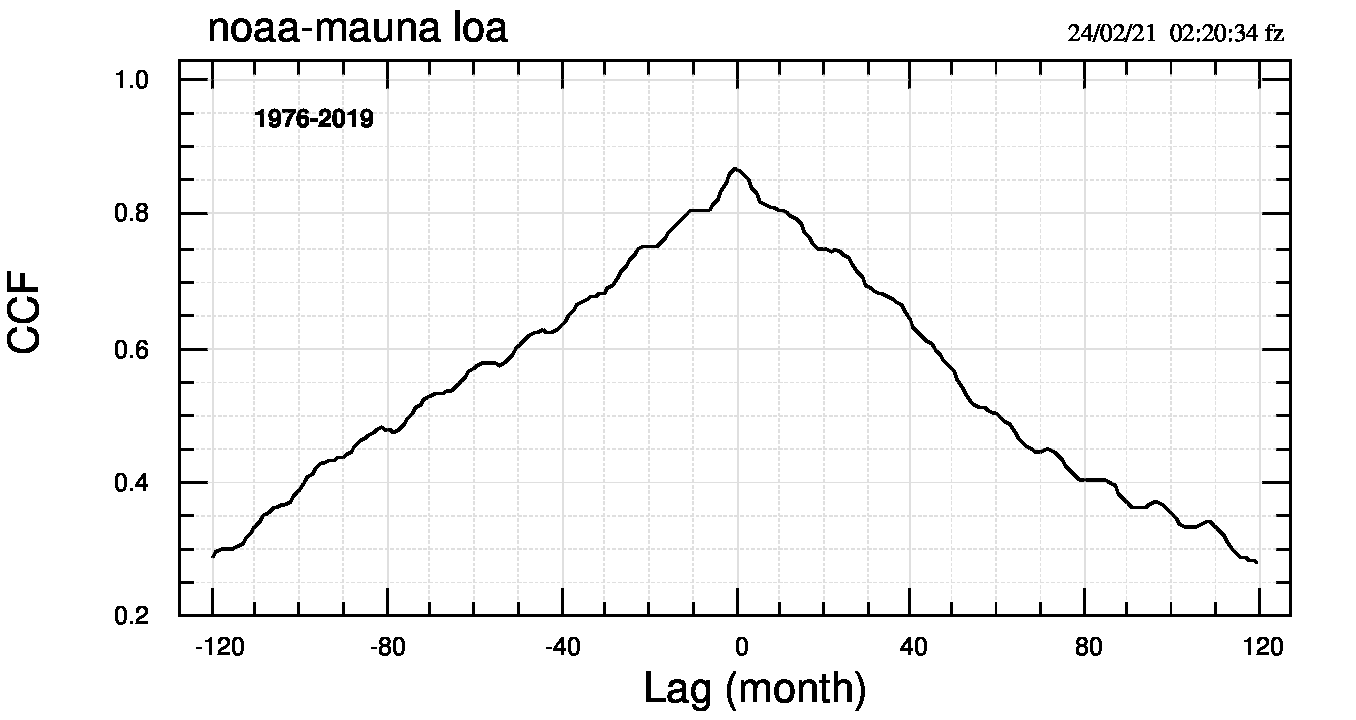
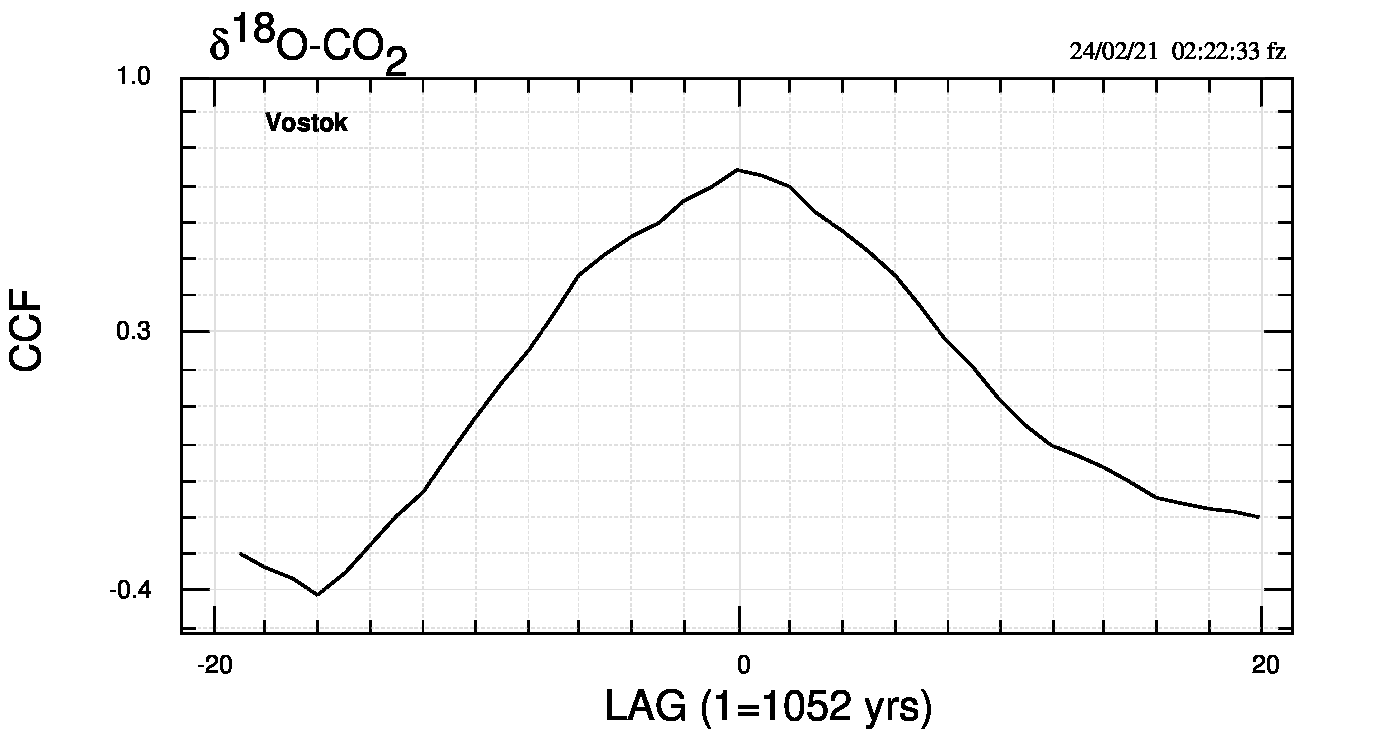
Nei due casi per i quali ho calcolato la funzione di cross-correlazione (CCF), e cioè 1976-2019 e “Vostok” (figure 2 e 3), non sembra esistere una evidente relazione tra chi precede e chi segue tra le due variabili.

Fig.2: Funzione di cross-correlazione (CCF) tra temperatura (GHCN) e CO2 (Mauna Loa) da cui non appare una serie che preceda o segua l’altra.

Fig.3: Funzione di cross-correlazione (CCF) tra le serie digitalizzate “Vostok”. Anche in questo caso non sembra che una serie preceda o segua l’altra. Qui un “lag” equivale a più di 1000 anni, il che non permette un confronto con maggiore dettaglio.

Commenti conclusivi
L’equazione (3) o (3a) sembra valida (quando è valida) solo in media, mentre la relazione puntuale “la CO2 aumenta e quindi la temperatura aumenta” non funziona, a prescindere dal È nato prima l’uovo o la gallina? (o quale delle due grandezze controlla l’altra), come si vede dai “ghirigori” di figura 1 ma anche dal periodo 1981-2012 della stessa figura, dove ad un continuo aumento di concentrazione di CO2 corrispondono alti e bassi di temperatura che, in tutta evidenza, seguono altre “logiche” rispetto al totale controllo da parte dell’anidride carbonica.
Le funzioni di cross-correlazione di una serie breve e una lunga non mostrano ritardi o anticipi di una variabile rispetto all’altra, anche se nel caso più esteso temporalmente la risoluzione potrebbe essere superiore ad un’eventuale differenza.

Bibliografia

W.J. Davis: The Relationship between Atmospheric Carbon Dioxide Concentration and Global Temperature for the Last 425 Million Years Climate, 5(4), 76-, 2017. https://doi.org/10.3390/cli5040076
https://www.ipcc.ch/site/assets/uploads/2018/07/WGI_AR5.Chap_.8_SM.pdf (IPCC WGI AR5, Chap. 8, SM: Anthropogenic and Natural Radiative Forcing, Supplementary Material)
Thorstein O. Seim, Borgar T. Olsen: The Influence of IR Absorption and Backscatter Radiation from CO2 on Air Temperature during Heating in a Simulated Earth/Atmosphere Experiment, Atmospheric and Climate Sciences, 10-2, 2020. https://doi.org/10.4236/acs.2020.102009

Tutti i dati e i grafici sono disponibili nel sito di supporto

Related Posts

You Missed